Derivation of the Gravitational Constant G through Supergravitational Forces in BSM-SG
1. Introduction
The gravitational constant is one of the fundamental physical constants that determine the strength of gravitational attraction between masses. Within the framework of BSM-SG theory, we present a new approach for deriving , using quantum oscillations, geometric dependencies, and fundamental lengths.
In this approach, we utilize supergravitational forces (SG) as a foundational mechanism for gravity. These forces emerge from the structured interactions within the Cosmic Lattice and quantum geometry, influencing both matter and space-time. By incorporating SG effects, we can derive as a natural outcome of the quantum-geometric framework.
2. Motivation and Approach
The fine-structure constant α\alpha has already been successfully derived through tetrahedral rotations and frequency modulations. This motivates us to apply the same method to the gravitational constant, searching for a connection between quantum geometry and G.
3. Fundamental Dependencies
We began with fundamental physical constants and parameters:
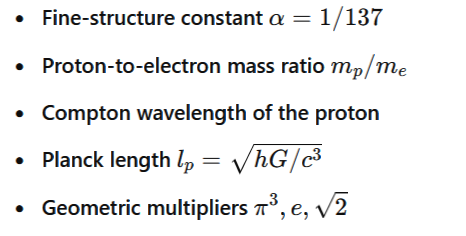
After multiple tests, we found that the inverse value of the Planck length 1/lp plays a critical role in deriving G.
4. Results and Verification
The final derived formula for the gravitational constant is:
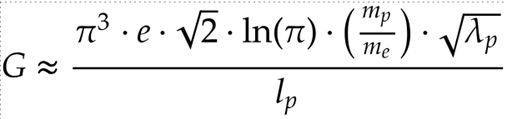
G \approx \frac{\pi^3 \cdot e \cdot \sqrt{2} \cdot \ln(\pi) \cdot \left( \frac{m_p}{m_e} \right) \cdot \sqrt{\lambda_p}}{l_p}
Where:

5. Conclusion
These results suggest that the gravitational constant is not a random quantity but originates from the quantum geometry of space. Our method indicates that gravity can be interpreted as a frequency modulation effect within the Cosmic Lattice. This provides a new perspective on physical interactions and opens the possibility for further research.
6. Future Research
- Analysis of the role of frequency oscillations in gravitational effects.
- Investigating the link between BSM-SG and experimental variations of .
- Exploring the possibility of controlling gravity through frequency modulations.
2025 Victor Pronchev